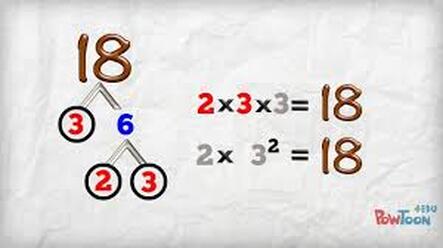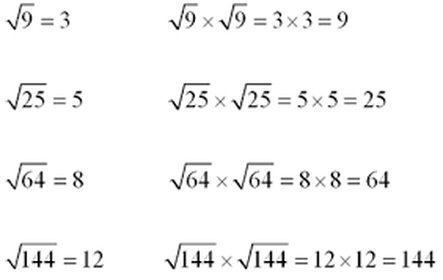welcome to math online class....
The Cambridge Lower Secondary Math curriculum framework focuses on principles, patterns, systems, functions and relationships so that learners can apply their mathematical knowledge and develop a holistic understanding of the subject. The Cambridge Lower Secondary Mathematics curriculum framework provides a solid foundation for further stages of education such as Cambridge IGCSE.
We organise the Cambridge Lower Secondary Mathematics curriculum in six content areas or ‘strands’. Each strand is further divided into ‘sub-strands’.
Number
• Integers, powers and roots.
• Place value, ordering and rounding.
• Fractions, decimals, percentages, ratio and proportion.
• Calculation.
Algebra
• Expressions, equations and formulae.
• Sequences, functions and graphs.
Geometry
•Shapes and geometric reasoning.
• Position and movement. Measure
• Length, mass and capacity.
• Times and rates of change.
• Area, perimeter and volume.
Handling data
• Planning and collecting data.
• Processing and presenting data.
• Interpreting and discussing results.
• Probability.
Problem solving
• Using techniques and skills in solving mathematical problems.
• Using understanding and strategies in solving problems.
We organise the Cambridge Lower Secondary Mathematics curriculum in six content areas or ‘strands’. Each strand is further divided into ‘sub-strands’.
Number
• Integers, powers and roots.
• Place value, ordering and rounding.
• Fractions, decimals, percentages, ratio and proportion.
• Calculation.
Algebra
• Expressions, equations and formulae.
• Sequences, functions and graphs.
Geometry
•Shapes and geometric reasoning.
• Position and movement. Measure
• Length, mass and capacity.
• Times and rates of change.
• Area, perimeter and volume.
Handling data
• Planning and collecting data.
• Processing and presenting data.
• Interpreting and discussing results.
• Probability.
Problem solving
• Using techniques and skills in solving mathematical problems.
• Using understanding and strategies in solving problems.
Class Rules:
Dear Students,
Greetings from Royal British International School!
My name is Ms.Gayatri Molli and I will be your Math Teacher.
Here are my contact details:
Email: [email protected]
Mobile:+959976495747 (What’s App only)
Rules:
WhatsApp groups are created in order to keep the avenues open with regards to communication. Effective communication is essential and WhatsApp has proven to be an ideal medium.
With these groups, however, comes the responsible use of its members.
Please take note of the following:
* NO messages are permitted to be posted before 8:00 am and after 8:00pm, seven days a week.
* NO general conversations. Please, rather chat to the person concerned via a private message instead of subjecting the group to long-winded chats on the group. It can become distracting and annoying to group member.
* NO harsh words, gossiping, unpleasant comments, online bullying or nastiness. These sort of issues should be brought directly to the homeroom teacher’s attention or the Schools Principal.
* Unless absolutely necessary, they are NOT a platform to help find lost property.
* They are NOT a platform to ask about what homework needs to be done. You are accountable for your own homework and your responsibility to submit it on time.
* This group is not a platform to air grievances or complaints; It would be preferred that members message the concerned person privately or speak to your homeroom teacher and /or School Principal.
* They are NOT a platform to post pictures that you feel your classmates may find funny or cute.
“Please remember, WhatsApp Groups are meant to be useful and certainly not something that proves to be irritating to members. Think before you type!”
Our first lesson will officially start on Tuesday. Looking forward to a fruitful and productive Academic year .
Stay Safe !
Ms.Gayatri Molli
Dear Students,
Greetings from Royal British International School!
My name is Ms.Gayatri Molli and I will be your Math Teacher.
Here are my contact details:
Email: [email protected]
Mobile:+959976495747 (What’s App only)
Rules:
WhatsApp groups are created in order to keep the avenues open with regards to communication. Effective communication is essential and WhatsApp has proven to be an ideal medium.
With these groups, however, comes the responsible use of its members.
Please take note of the following:
* NO messages are permitted to be posted before 8:00 am and after 8:00pm, seven days a week.
* NO general conversations. Please, rather chat to the person concerned via a private message instead of subjecting the group to long-winded chats on the group. It can become distracting and annoying to group member.
* NO harsh words, gossiping, unpleasant comments, online bullying or nastiness. These sort of issues should be brought directly to the homeroom teacher’s attention or the Schools Principal.
* Unless absolutely necessary, they are NOT a platform to help find lost property.
* They are NOT a platform to ask about what homework needs to be done. You are accountable for your own homework and your responsibility to submit it on time.
* This group is not a platform to air grievances or complaints; It would be preferred that members message the concerned person privately or speak to your homeroom teacher and /or School Principal.
* They are NOT a platform to post pictures that you feel your classmates may find funny or cute.
“Please remember, WhatsApp Groups are meant to be useful and certainly not something that proves to be irritating to members. Think before you type!”
Our first lesson will officially start on Tuesday. Looking forward to a fruitful and productive Academic year .
Stay Safe !
Ms.Gayatri Molli
section 1 term 1 topics
Section 1
Chapter 1 Place value, ordering and rounding
Chapter 2 Expressions
Chapter 3 Shapes and geometric reasoning
Chapter 4 Length, mass and capacity
Chapter 5 Collecting and displaying data
Chapter 6 Addition and subtraction
Chapter 7 ICT, investigations and problem solving
Chapter 1 Place value, ordering and rounding
Chapter 2 Expressions
Chapter 3 Shapes and geometric reasoning
Chapter 4 Length, mass and capacity
Chapter 5 Collecting and displaying data
Chapter 6 Addition and subtraction
Chapter 7 ICT, investigations and problem solving
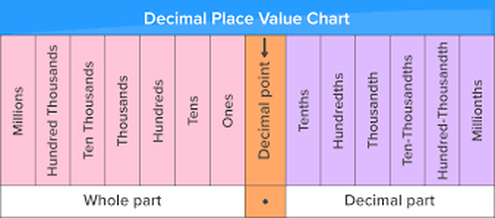
Chapter:1 Place Value,Ordering and Rounding
Learning Objectives: Read and write numbers up to 1 million Know what each digit represents in whole numbers up to a million
Ordering Place Value
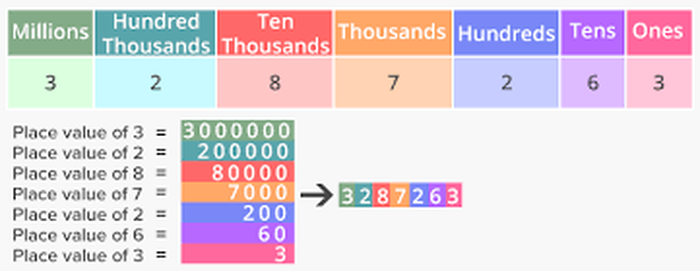
Numbers, such as 495,784, have six digits. Each digit is a different place value.
The first digit is called the hundred thousands' place. It tells you how many sets of one hundred thousand are in the number. The number 495,784 has four hundred thousands.
The second digit is the ten thousands' place. In this number there are nine ten thousands in addition to the four hundred thousands.
The third digit is the one thousands' place which is five in this example. Therefore there are four sets of one hundred thousand, nine sets of ten thousand, and five sets of one thousand in the number 495,784.
The fourth digit is called the hundreds' place. It tells how many sets of one hundred are in the number. The number 495,784 has seven hundreds in addition to the thousands.
The next digit is the tens' place. This number has are eight tens in addition to the four hundred thousands, nine ten thousands, five thousands and seven hundreds.
The last or right digit is the ones' place which is four in this example. Therefore there are four sets of one hundred thousand, nine sets of ten thousand, five sets of one thousand, seven sets of one hundred, eight sets of ten, and four ones in the number 495,784
Numbers, such as 495,784, have six digits. Each digit is a different place value.
The first digit is called the hundred thousands' place. It tells you how many sets of one hundred thousand are in the number. The number 495,784 has four hundred thousands.
The second digit is the ten thousands' place. In this number there are nine ten thousands in addition to the four hundred thousands.
The third digit is the one thousands' place which is five in this example. Therefore there are four sets of one hundred thousand, nine sets of ten thousand, and five sets of one thousand in the number 495,784.
The fourth digit is called the hundreds' place. It tells how many sets of one hundred are in the number. The number 495,784 has seven hundreds in addition to the thousands.
The next digit is the tens' place. This number has are eight tens in addition to the four hundred thousands, nine ten thousands, five thousands and seven hundreds.
The last or right digit is the ones' place which is four in this example. Therefore there are four sets of one hundred thousand, nine sets of ten thousand, five sets of one thousand, seven sets of one hundred, eight sets of ten, and four ones in the number 495,784
Ordering Numbers
Numbers have an order or arrangement. The number two is between one and three. Three or more numbers can be placed in order. A number may come before the other numbers or it may come between them or after them.
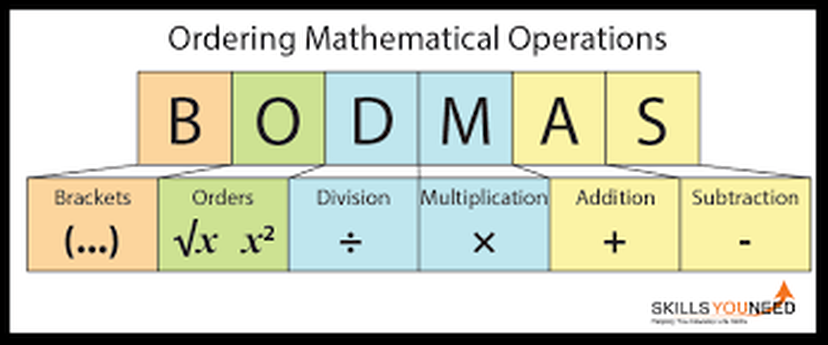
BODMAS is a useful acronym that lets you know which order to solve mathematical problems (or sums). It's important that you follow the rules of BODMAS as without it your answers can be wrong.
The BODMAS acronym is for:
Numbers have an order or arrangement. The number two is between one and three. Three or more numbers can be placed in order. A number may come before the other numbers or it may come between them or after them.
BODMAS is a useful acronym that lets you know which order to solve mathematical problems (or sums). It's important that you follow the rules of BODMAS as without it your answers can be wrong.
The BODMAS acronym is for:
- Brackets (parts of a calculation inside brackets always come first).
- Orders (numbers involving powers or square roots).
- Division.
- Multiplication.
- Addition.
- Subtraction
- Brackets:
Start with anything inside brackets, going from left to right.
Example:4 × (3 + 2) = ?
You need to do the operation, or sum, inside the brackets first, 3 + 2, then multiply the answer by 4.
3 + 2 = 5.
4 × 5 = 20
If you ignored the brackets and did the sum 4 × 3 + 2 you would get 14. You can see how the brackets make a difference to the answer. - Orders:
Do anything involving a power or a square root next (these are also known as orders), again working from left to right if there is more than one.
Example:32 + 5 = ?
You need to do the power sum first, before you can add 5.
32 = 3 × 3 = 9
9 + 5 = 14 - Division and Multiplication:
Once you have done any parts of the sum involving brackets or powers the next step is division and multiplication.
Multiplication and division rank equally, so you go from left to right in the sum, doing each operation in the order in which it appears.
Example:4 × 5 ÷ 2 + 7 = ?
You need to do division and multiplication first, but you have one of each.
Start from the left and work across to the right, which means that you start with 4 × 5 = 20. Then do the division, 20 ÷ 2 = 10.
Only then do you move to the addition: 10 + 7 = 17. The answer is 17. - Addition and Subtraction
The final step is to calculate any addition or subtraction. Again, subtraction and addition rank equally, and you simply move from left to right.
Example:4 + 6 - 7 + 3 = ?
You simply start on the left and work your way across.
4 + 6 = 10
10 - 7 = 3
3 + 3 = 6
The answer is 6.
|
|
|
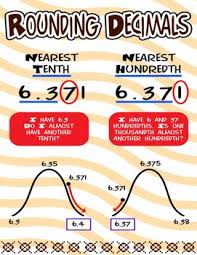
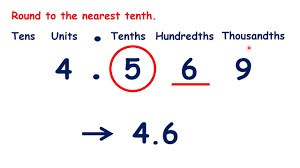
Rounding
A rounded number has about the same value as the number you start with, but it is less exact.
For example, 341 rounded to the nearest hundred is 300. That is because 341 is closer in value to 300 than to 400. When rounding off to the nearest dollar, $1.89 becomes $2.00, because $1.89 is closer to $2.00 than to $1.00
Rules for RoundingHere's the general rule for rounding:
Consider the number 4,827.
A rounded number has about the same value as the number you start with, but it is less exact.
For example, 341 rounded to the nearest hundred is 300. That is because 341 is closer in value to 300 than to 400. When rounding off to the nearest dollar, $1.89 becomes $2.00, because $1.89 is closer to $2.00 than to $1.00
Rules for RoundingHere's the general rule for rounding:
- If the number you are rounding is followed by 5, 6, 7, 8, or 9, round the number up. Example: 38 rounded to the nearest ten is 401
- If the number you are rounding is followed by 0, 1, 2, 3, or 4, round the number down. Example: 33 rounded to the nearest ten is 30
Consider the number 4,827.
- 4,827 rounded to the nearest ten is 4,830
- 4,827 rounded to the nearest hundred is 4,800
- 4,827 rounded to the nearest thousand is 5,000
- 34 rounded to the nearest ten is 30
- 6,809 rounded to the nearest hundred is 6,800
- 1,951 rounded to the nearest thousand is 2,000
worksheets
|
|
| ||||||||||||||||||||||||
|
|
| ||||||||||||||||||
chapter-2 Expressions
What is an expression ?
Numbers, symbols and operators (such as + and ×) grouped together that show the value of something. Examples: 2 + 3 is an expression.
How do you solve an expression?
Solve an algebraic expression with fractions.
An expression is a number, a variable, or a combination of numbers and variables and operation symbols. An equation is made up of two expressions connected by an equal sign.
Numbers, symbols and operators (such as + and ×) grouped together that show the value of something. Examples: 2 + 3 is an expression.
How do you solve an expression?
Solve an algebraic expression with fractions.
- (x + 3)/6 = 2/3. First, cross multiply to get rid of the fraction. ...
- (x + 3) x 3 = 2 x 6 =
- 3x + 9 = 12. Now, combine like terms. ...
- 3x + 9 - 9 = 12 - 9 =
- 3x = 3. Isolate the variable, x, by dividing both sides by 3 and you've got your answer.
- 3x/3 = 3/3 =
- x =1.
An expression is a number, a variable, or a combination of numbers and variables and operation symbols. An equation is made up of two expressions connected by an equal sign.
What is an Expression?
An expression is a sentence with a minimum of two numbers and at least one math operation.
This math operation can be addition, subtraction, multiplication, and division. The structure of an expression is:
Expression = (Number, Math Operator, Number)
For example,
= 7 + 9
= 23 × 4
= 37 – 6
= 25 + 9 – 4 ÷ 2
In all the given expressions, a math operator is used between the two numbers.
A math expression is different from a math equation. An equation will always use an equivalent (=) operator between two math expressions.
The structure of defining math expression advances in different grades. In early grades, children are expected to write math expressions using numbers and operators. Later on, words help students to form a math expression.
Let’s consider a word problem.
Tom has to fill a box with oranges and apples. The number of apples should be 5 more than oranges. Tom picks 3 oranges each time and repeats it 5 times. Count the total number of oranges and apples.
To solve this, formulate the math expressions as follows:
= Number of oranges = 3 × 5
= Number of oranges = 15
Number of apples = Number of oranges + 5
= Number of apples = 15 + 5
= Number of apples = 20
Total number of fruits = Number of oranges + Number of apples
Third math expression will be:
= 15 + 20
= 35
What is Numerical Expression?
The term numerical expression is made up of two words, numerical meaning numbers, and expression meaning phrase. Thus, it is a phrase involving numbers.
A numerical expression in mathematics can be a combination of numbers, integers combined using mathematical operators such as addition, subtraction, multiplication, or division.
Examples of Numerical Expressions
We can form a numerical expression by combining numbers with various mathematical operators. There is no limit to the number of operators a numerical expression may contain. Some numerical expressions use only one operator between two numbers, and some may contain more.
Some examples of numerical expression are given below:
10 + 5
250 - 75
60 × 5 + 10
72 ÷ 8 × 5 - 4 + 1
82 + 4 - 10
Writing Numerical expression Any mathematical word problem is solved by first converting into a numerical expression.
Below are some examples.
Candice has 10 chocolate bars. She gives 3 to her sister, 1 to her friend and eats 2 of them. Later she visits her grandmother, and she (grandmother) offers Candice 12 more chocolate bars. How many chocolate bars does Candice have now?
Let’s look at the numbers involved in the above problem. Candice starts with 10 bars, gives away 4 (3+1), eats 2 and then again gets 12 more from her grandmother. So, the numerical expression is
10 - 3 - 1 - 2 + 12
= 7 - 1 - 2 + 12
= 6 - 2 + 12
= 4 + 12
= 16
This gives us 16.
Fun Facts
- A power is also a numerical expression that has two parts: an exponent and a base.
- An expression can also be a combination of variables and constants, combined using mathematical operations. Such an expression is known as an algebraic expression.
How to write an equation
worksheets
|
| ||||||||||||
| evaluating_expressions.pdf | |
| File Size: | 35 kb |
| File Type: | |
| lineqnvarbothsides.pdf | |
| File Size: | 5 kb |
| File Type: | |
| algebraic_expressions_packet__study_guide__2.pdf | |
| File Size: | 1649 kb |
| File Type: | |
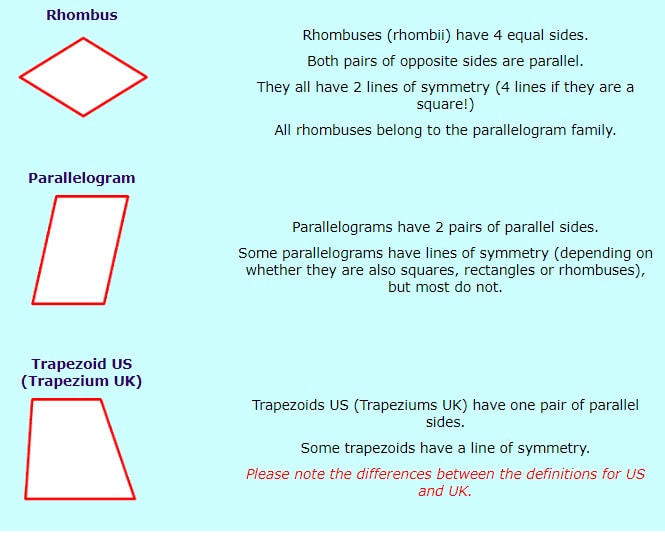
Chapter3-Shapes and Geometric reasoning
A reflection is the flipping of a point or figure over a line of reflection (the mirror line). A rotation is the turning of a figure or object around a fixed point.
Reflection is flipping an object across a line without changing its size or shape. Rotation is rotating an object about a fixed point without changing its size or shape. Translation is sliding a figure in any direction without changing its size, shape or orientation.
What are the 4 types of transformations?
There are four main types of transformations: translation, rotation, reflection and dilation.
How do you rotate a shape?
Rotating a shape 90 degrees is the same as rotating it 270 degrees clockwise. The convention is that when rotating shapes on a coordinate plane, they rotate counterclockwise, or towards the left. You should assume this, unless it is noted in the problem that you need to rotate clockwise.
Reflection is flipping an object across a line without changing its size or shape. Rotation is rotating an object about a fixed point without changing its size or shape. Translation is sliding a figure in any direction without changing its size, shape or orientation.
What are the 4 types of transformations?
There are four main types of transformations: translation, rotation, reflection and dilation.
How do you rotate a shape?
Rotating a shape 90 degrees is the same as rotating it 270 degrees clockwise. The convention is that when rotating shapes on a coordinate plane, they rotate counterclockwise, or towards the left. You should assume this, unless it is noted in the problem that you need to rotate clockwise.
WORKSHEETS
| trans1.pdf | |
| File Size: | 30 kb |
| File Type: | |
| rotations_of_shapes.pdf | |
| File Size: | 47 kb |
| File Type: | |
| reflection-shapes-2.pdf | |
| File Size: | 76 kb |
| File Type: | |
| reflection-shapes-1.pdf | |
| File Size: | 76 kb |
| File Type: | |
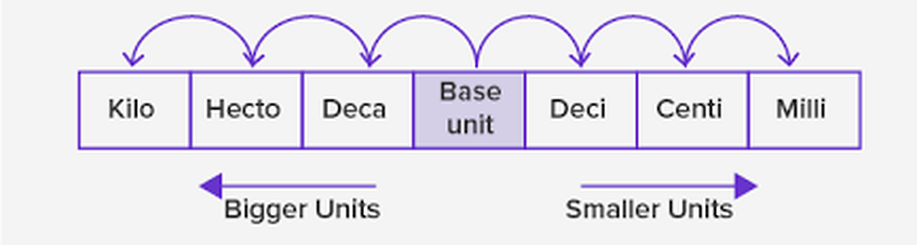
chapter- 4 LENGTH, MASS AND CAPACITY
What is length mass and capacity?
In the metric system, the base unit of length is the meter (m).
The base unit of mass is the gram (g). The base unit of capacity is the liter (L).
For example,
there are 100 centimeters in 1 meter.
“kilo” means one thousand
What are the measurements of capacity?
Capacity is measured in the SI base unit called litres (L).
The most common units for capacity are litre (L) and millilitre (mL).
What are the measurements of length?
length is measured in the SI base unit called kilometres(km).
The most common units for length are millimeter(mm), centimeter(cm), meter(m) and kilometer(km).
What are the measurements of mass?
mass is measured in the SI base unit called kilogram(kg).
The most common units for capacity are grams(g) and kilograms(kg).
In the metric system, the base unit of length is the meter (m).
The base unit of mass is the gram (g). The base unit of capacity is the liter (L).
For example,
there are 100 centimeters in 1 meter.
“kilo” means one thousand
What are the measurements of capacity?
Capacity is measured in the SI base unit called litres (L).
The most common units for capacity are litre (L) and millilitre (mL).
What are the measurements of length?
length is measured in the SI base unit called kilometres(km).
The most common units for length are millimeter(mm), centimeter(cm), meter(m) and kilometer(km).
What are the measurements of mass?
mass is measured in the SI base unit called kilogram(kg).
The most common units for capacity are grams(g) and kilograms(kg).
|
|
|
chapter-4 worksheets
| ch-4.1.pdf | |
| File Size: | 22 kb |
| File Type: | |
| ch-4.2.pdf | |
| File Size: | 22 kb |
| File Type: | |
| metric_pdf.pdf | |
| File Size: | 506 kb |
| File Type: | |
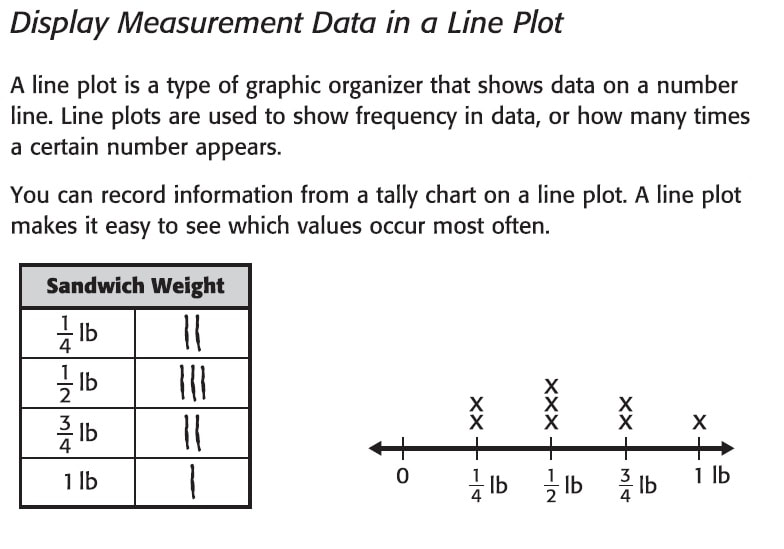
chapter-5 collecting and displaying data
video on tally chart
Data collecting chapter in detail and worksheets
| collect_and_display_data.pdf | |
| File Size: | 861 kb |
| File Type: | |
Chapter 6 Addition and subtraction
Chapter-8 integers Powers and Roots
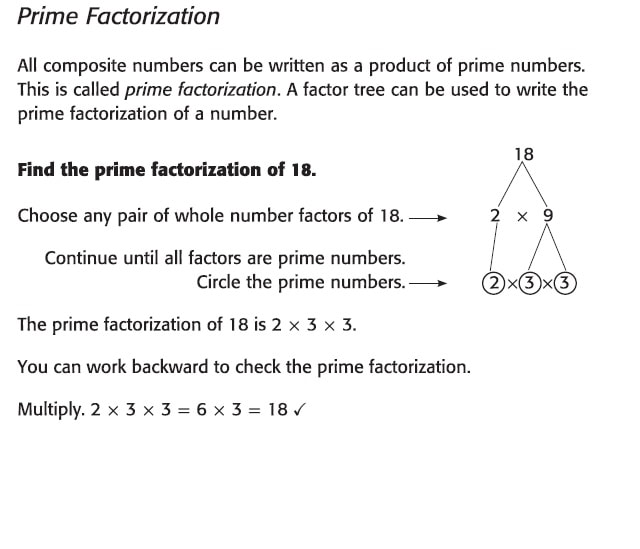
Prime factorization is to write a composite whole number as the product of prime numbers only. 1) 6 = 2 × 3 the factors 2 and 3 are prime numbers. 2) 12 = 2 × 2 × 3 the factors 2 and 3 are prime numbers.
"Prime Factorization" is finding which prime numbers multiply together to make the original number.
What is the prime factorisation of 24?
Answer and Explanation:
The prime factorization of the number 24 is 2 × 2 × 2 × 3.
"Prime Factorization" is finding which prime numbers multiply together to make the original number.
What is the prime factorisation of 24?
Answer and Explanation:
The prime factorization of the number 24 is 2 × 2 × 2 × 3.
Worksheet on prime factorization
Powers and exponents
Worksheets on Powers and exponents
| exponent_worksheet.pdf | |
| File Size: | 11 kb |
| File Type: | |
| exponent_worksheet__1_.pdf | |
| File Size: | 10 kb |
| File Type: | |
Integers
What is integers and example?
An integer includes whole numbers and negative whole numbers. Integers can be positive, negative, or zero. For example: 1, -1, 0, 101 and -101.
What is an integer in simple terms?
An integer (from the Latin integer meaning "whole") is colloquially defined as a number that can be written without a fractional component. For example, 21, 4, 0, and −2048 are integers, while 9.75, 512, and √2 are not.
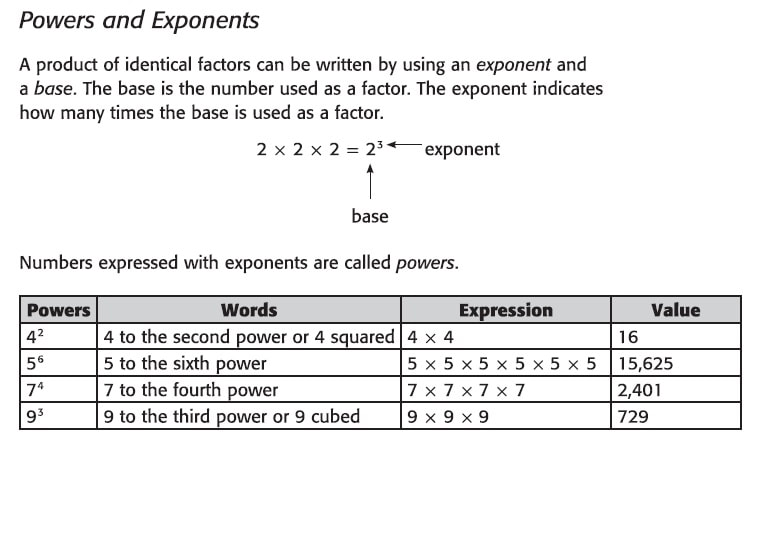
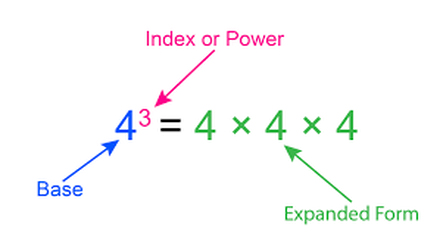
What is a power in math?
An expression that represents repeated multiplication of the same factor is called a power. The number 5 is called the base, and the number 2 is called the exponent. The exponent corresponds to the number of times the base is used as a factor.
How do you find the power in math?
If n is a positive integer and x is any real number, then xn corresponds to repeated multiplication xn=x×x×⋯×x⏟n times.
What are power numbers?
The power (or exponent) of a number says how many times to use the number in a multiplication. It is written as a small number to the right and above the base number. In this example the little "2" says to use 8 two times in a multiplication: 82 = 8 × 8 = 64.
a square is the result of multiplying a number by itself. The verb "to square" is used to denote this operation. Squaring is the same as raising to the power 2, and is denoted by a superscript 2; for instance, the square of 3 may be written as 32, which is the number 9.
What does ² mean?
In math, the squared symbol (2) is an arithmetic operator that signifies multiplying a number by itself. The “square” of a number is the product of the number and itself. Multiplying a number by itself is called “squaring” the number.
What is the square number of?
In mathematics, a square number or perfect square is an integer that is the square of an integer; in other words, it is the product of some integer with itself. For example, 9 is a square number, since it can be written as 3 × 3.
An integer includes whole numbers and negative whole numbers. Integers can be positive, negative, or zero. For example: 1, -1, 0, 101 and -101.
What is an integer in simple terms?
An integer (from the Latin integer meaning "whole") is colloquially defined as a number that can be written without a fractional component. For example, 21, 4, 0, and −2048 are integers, while 9.75, 512, and √2 are not.
What is a power in math?
An expression that represents repeated multiplication of the same factor is called a power. The number 5 is called the base, and the number 2 is called the exponent. The exponent corresponds to the number of times the base is used as a factor.
How do you find the power in math?
If n is a positive integer and x is any real number, then xn corresponds to repeated multiplication xn=x×x×⋯×x⏟n times.
What are power numbers?
The power (or exponent) of a number says how many times to use the number in a multiplication. It is written as a small number to the right and above the base number. In this example the little "2" says to use 8 two times in a multiplication: 82 = 8 × 8 = 64.
a square is the result of multiplying a number by itself. The verb "to square" is used to denote this operation. Squaring is the same as raising to the power 2, and is denoted by a superscript 2; for instance, the square of 3 may be written as 32, which is the number 9.
What does ² mean?
In math, the squared symbol (2) is an arithmetic operator that signifies multiplying a number by itself. The “square” of a number is the product of the number and itself. Multiplying a number by itself is called “squaring” the number.
What is the square number of?
In mathematics, a square number or perfect square is an integer that is the square of an integer; in other words, it is the product of some integer with itself. For example, 9 is a square number, since it can be written as 3 × 3.
| int1.pdf | |
| File Size: | 24 kb |
| File Type: | |
| int2.pdf | |
| File Size: | 28 kb |
| File Type: | |
| int3.pdf | |
| File Size: | 29 kb |
| File Type: | |
POWERS AND ROOTS
What are powers and root?
A power of a number is a number raised to another number and takes on the form ab. To calculate powers of numbers, we multiply a (also called the base) by itself b (also called the power or exponent) times. The nth root of x is the number that we need to multiply by itself n times in order to get x.
How do you estimate roots and powers?
Estimating powers and roots
How to Convert Square Roots to Exponents
Every non negative real number x has a unique non negative square root, called the principal square root, which is denoted by √x, where the symbol √ is called the radical.
For example,
The principal square root of 9 is 3, which is denoted by √9 = 3, because 32 = 3 ⋅
3 = 9 and 3 is non negative.
A power of a number is a number raised to another number and takes on the form ab. To calculate powers of numbers, we multiply a (also called the base) by itself b (also called the power or exponent) times. The nth root of x is the number that we need to multiply by itself n times in order to get x.
How do you estimate roots and powers?
Estimating powers and roots
- Powers of any number can be estimated by finding the nearest integers above and below the number.
- Estimate the value of 3.7 3
- 3.7 is between 3 and 4. ...
- Roots can be estimated by finding the roots of numbers that have integer values above and below the number.
- Estimate the value of √53.
How to Convert Square Roots to Exponents
- The nth root of a can be written as a fractional exponent with a raised to the reciprocal of that power.
- When the nth root of.
- is taken, it's raised to the 1/n power. When a power is raised to another power, you multiply the powers together, and so the m (otherwise written as m/1) and the 1/n are multiplied together.
Every non negative real number x has a unique non negative square root, called the principal square root, which is denoted by √x, where the symbol √ is called the radical.
For example,
The principal square root of 9 is 3, which is denoted by √9 = 3, because 32 = 3 ⋅
3 = 9 and 3 is non negative.
Square root
| square_roots_worksheet.pdf | |
| File Size: | 10 kb |
| File Type: | |
| square_roots_worksheet__1_.pdf | |
| File Size: | 11 kb |
| File Type: | |
| power_2.pdf | |
| File Size: | 12 kb |
| File Type: | |
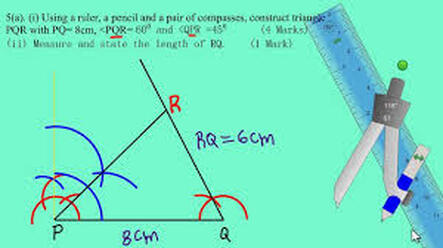
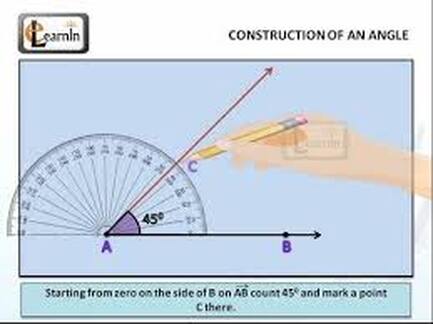
chapter-10 Measurement and construction
How to construct angles
worksheets:
| drawing-angles-five-degree-increments.pdf | |
| File Size: | 129 kb |
| File Type: | |
| drawing-angles-inner-outer-scales.pdf | |
| File Size: | 97 kb |
| File Type: | |
| using-own-protractor.pdf | |
| File Size: | 49 kb |
| File Type: | |
unit - 11 TIME

In math, time can be defined as the ongoing and continuous sequence of events that occur in succession, from the past through the present to the future. ... We measure and define what time of the day it is using clocks. A clock in general has 12 numbers written on it, from 1 to 12.
How can you measure time?
Time is measured with instruments such as a clock or calendar. These instruments can be anything that exhibits two basic components: (1) a regular, constant, or repetitive action to mark off equal increments of time, and (2) a means of keeping track of the increments of time and of displaying the result.
How do you make a clock in math?
Every time we go past 12 on the clock we start counting the hours at 1 again. If we add numbers the way we add hours on the clock, we say that we are doing clock arithmetic. So, in clock arithmetic 8 + 6 = 2, because 6 hours after 8 o'clock is 2 o'clock.
How can you measure time?
Time is measured with instruments such as a clock or calendar. These instruments can be anything that exhibits two basic components: (1) a regular, constant, or repetitive action to mark off equal increments of time, and (2) a means of keeping track of the increments of time and of displaying the result.
How do you make a clock in math?
Every time we go past 12 on the clock we start counting the hours at 1 again. If we add numbers the way we add hours on the clock, we say that we are doing clock arithmetic. So, in clock arithmetic 8 + 6 = 2, because 6 hours after 8 o'clock is 2 o'clock.
Worksheet on Word Problems on Measurement of Time
1. A bus leaves for Rampur at 4:30 p.m. It takes 1 hr. 25 min. to reach there. At what time will it reach at Rampur?
2. The duration of a film show is 3 hr. 15 min. It starts at 6:30 p.m. When will it end?
3. The Punjab Mail arrived at Lucknow at 11:55 a.m. It reached at Lucknow 1 hr. 25 min. late. What is the scheduled arrival time of the train at Lucknow?
4. Rex visited a fashion show. He stayed there for 2 hr. 30 min. and came back at home. If he reached in the fashion show at 8:45 p.m. when did he leave for his home?
5. Max travelled 2 hr. 45 min. by bus and 4 hr. 45 min. by train. Calculate the time he spent in travelling.
6. David left home at 4:30 p.m. to meet his friend. He came back after 3 hr. 25 min. At what time did he came back?
7. Mary reached her school at 7:30 a.m. and left for home at 12:45 p.m. How long did she stay in school?
8. A circus show started at 6:15 p.m. and ended at 9:30 p.m. What was the duration of the show?
9. Sara started her homework at 5:30 p.m. and finished it at 9:15 p.m. How much time did she take to finish her homework?
10. Adrian studies 3 hr. 45 min. He starts studying at 8:05 p.m. At what time does he finish?
11. A school starts at 8:00 a.m. and closes at 12:45 a.m. How long does it work?
12. Jack left for Jaunpur at 4:30 a.m. He reached there at 11:55 a.m. How much time did he take to reach there?
13. Shelly started playing at 5:05 p.m. She played till 8: 15 p.m. How long did she play?
14. Maya started to draw a picture at 2:45 p.m. She completed it at 4:35 p.m. How much time did she take to draw the picture?
15. Aaron watched a cricket match from 10:15 a.m. to 11:50 a.m. and again from 2:30 p.m. How long did he watch the match in all?
1. A bus leaves for Rampur at 4:30 p.m. It takes 1 hr. 25 min. to reach there. At what time will it reach at Rampur?
2. The duration of a film show is 3 hr. 15 min. It starts at 6:30 p.m. When will it end?
3. The Punjab Mail arrived at Lucknow at 11:55 a.m. It reached at Lucknow 1 hr. 25 min. late. What is the scheduled arrival time of the train at Lucknow?
4. Rex visited a fashion show. He stayed there for 2 hr. 30 min. and came back at home. If he reached in the fashion show at 8:45 p.m. when did he leave for his home?
5. Max travelled 2 hr. 45 min. by bus and 4 hr. 45 min. by train. Calculate the time he spent in travelling.
6. David left home at 4:30 p.m. to meet his friend. He came back after 3 hr. 25 min. At what time did he came back?
7. Mary reached her school at 7:30 a.m. and left for home at 12:45 p.m. How long did she stay in school?
8. A circus show started at 6:15 p.m. and ended at 9:30 p.m. What was the duration of the show?
9. Sara started her homework at 5:30 p.m. and finished it at 9:15 p.m. How much time did she take to finish her homework?
10. Adrian studies 3 hr. 45 min. He starts studying at 8:05 p.m. At what time does he finish?
11. A school starts at 8:00 a.m. and closes at 12:45 a.m. How long does it work?
12. Jack left for Jaunpur at 4:30 a.m. He reached there at 11:55 a.m. How much time did he take to reach there?
13. Shelly started playing at 5:05 p.m. She played till 8: 15 p.m. How long did she play?
14. Maya started to draw a picture at 2:45 p.m. She completed it at 4:35 p.m. How much time did she take to draw the picture?
15. Aaron watched a cricket match from 10:15 a.m. to 11:50 a.m. and again from 2:30 p.m. How long did he watch the match in all?
Chapter 12 Averages
Chapter 13-Multiplication and Division
Multiplying decimals by whole numbers
| Multiplication and Division . pdf | |
| File Size: | 388 kb |
| File Type: | |
Chapter 15 Fractions,decimals and percentages
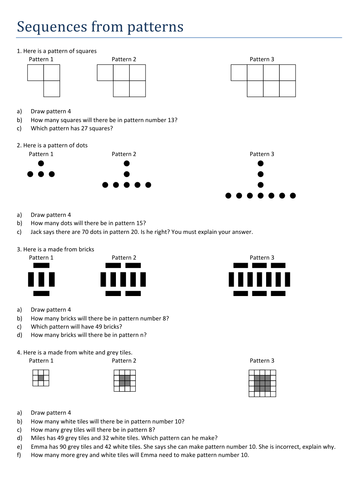
Chapter 16- Sequences:
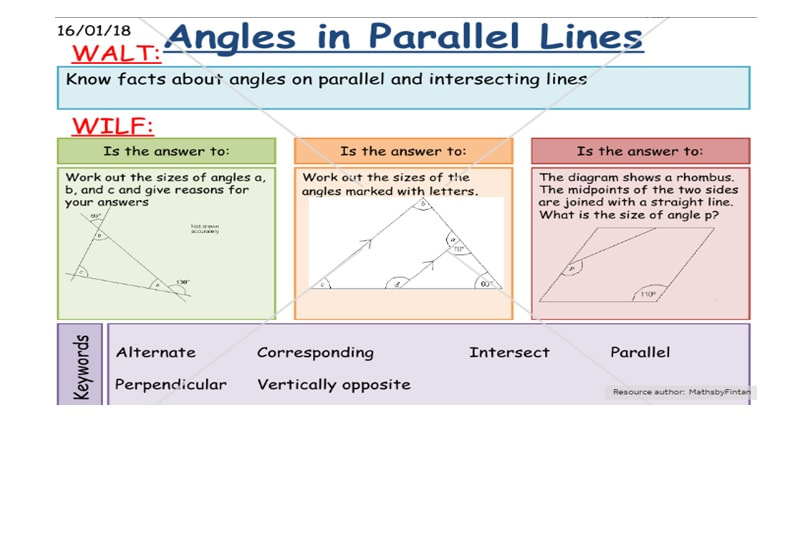
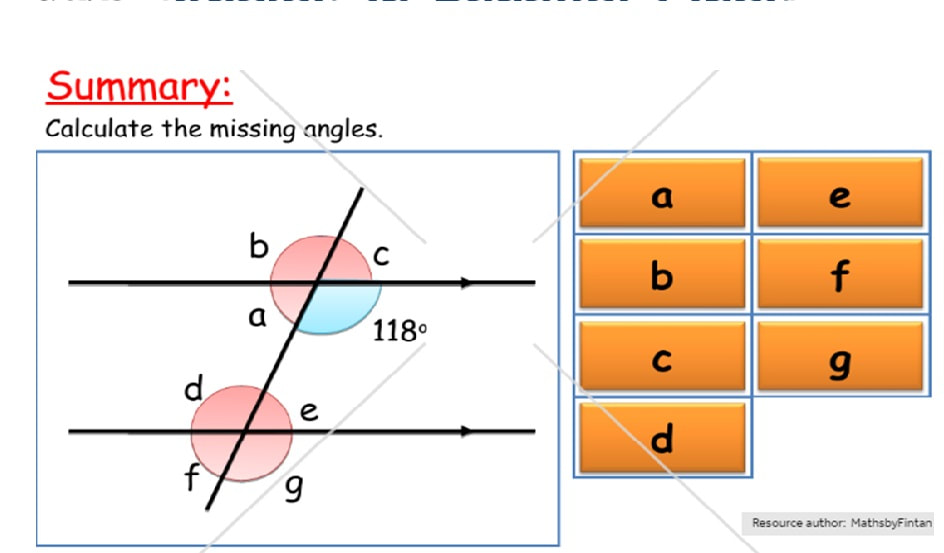
Chapter 17 - Angle properties
find the missing angles in the given quadrilaterals
| angles-in-a-quadrilateral-1.pdf | |
| File Size: | 149 kb |
| File Type: | |
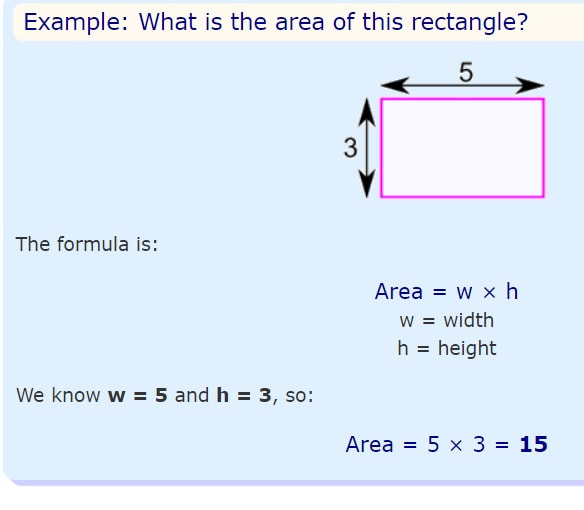
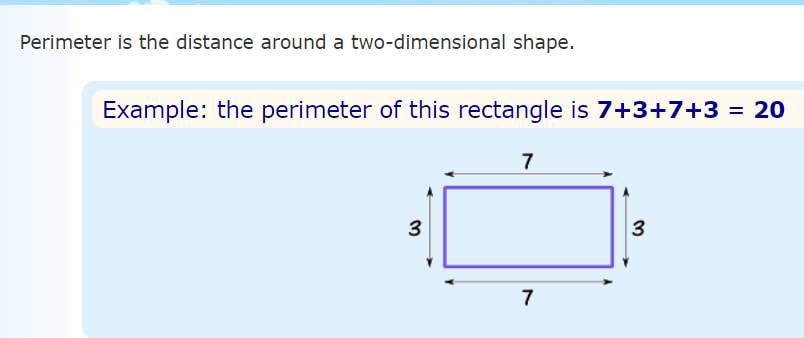
Chapter 18 Area and Perimeter of rectangles
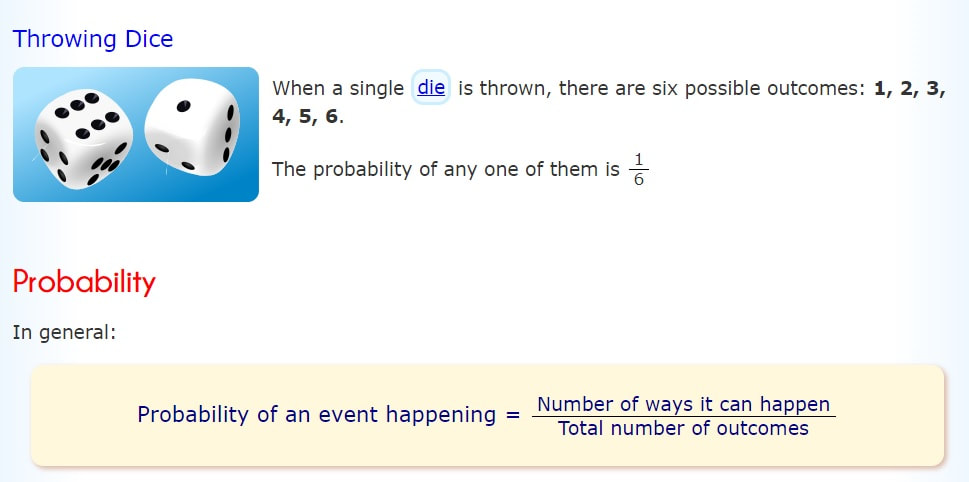
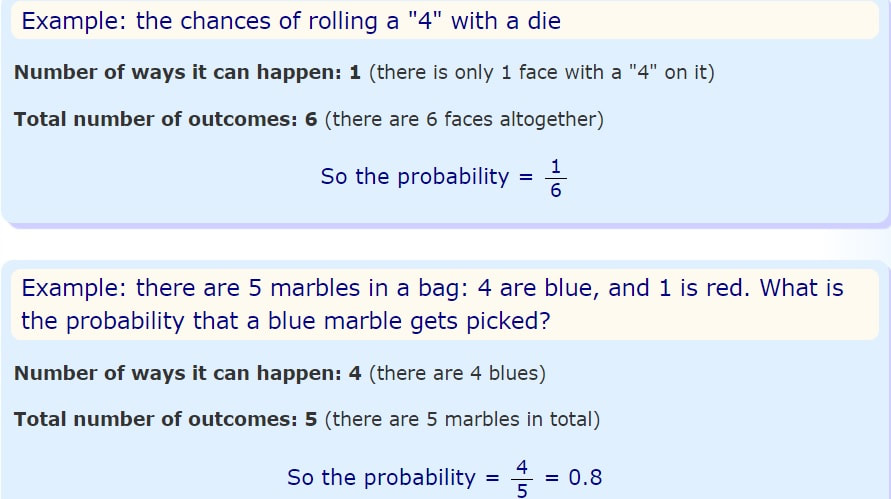
Chapter 19 probability
Chapter 20-Multiplication and division -2
Chapter 21 ICT investigations and problem solving
Chapter 22-Ratio and Proportion
Chapter 23 Formulae and substitution
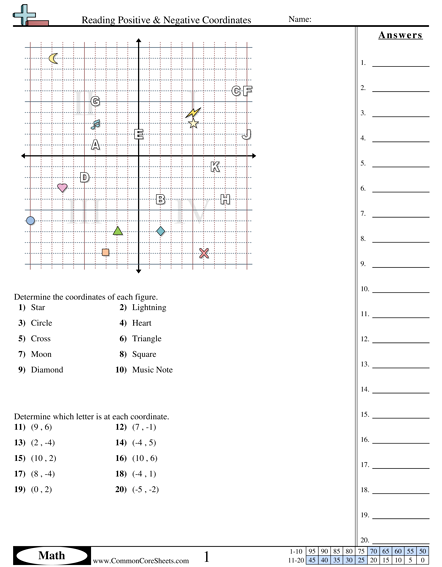
Chapter 24 Coordinates
Drag the points - game
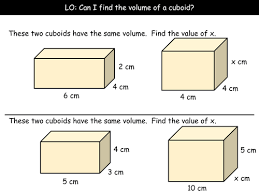
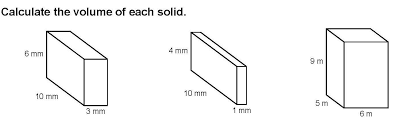
Chapter 25- Cubes and cuboids
| volume-of-a-cuboid-pdf1.pdf | |
| File Size: | 695 kb |
| File Type: | |
| volume_of_cubes_and_prisms.pdf | |
| File Size: | 1439 kb |
| File Type: | |
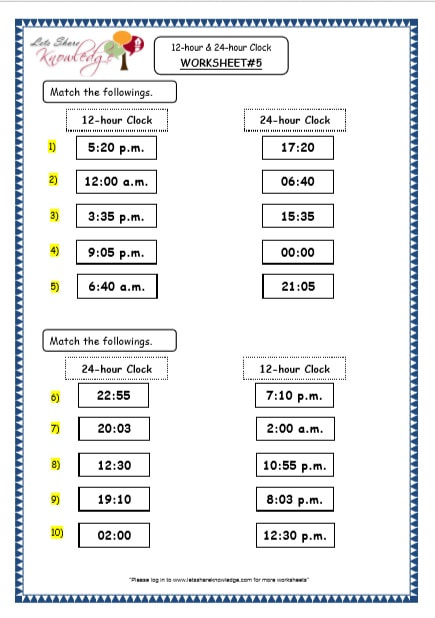
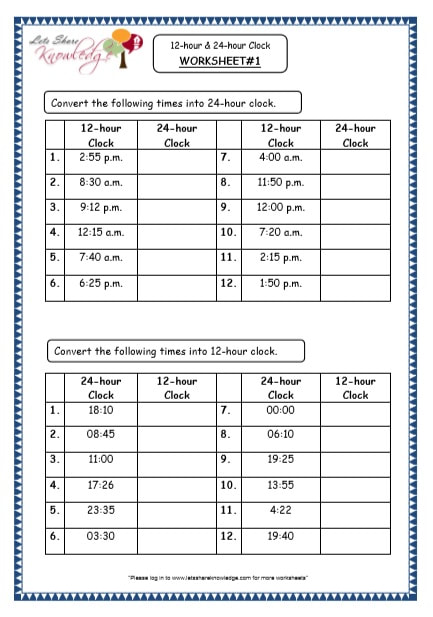
recall chapter-11
The 12 hour and 24 hour clocks
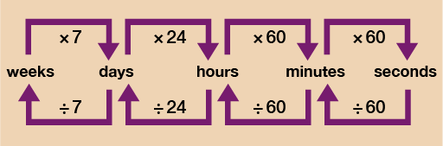
The system used in the modern world is as follows :
60 seconds is one minute,
60 minutes is one hour,
24 hours in one day.
There are two common ways of describing the time of day: the 12-hour clock and 24-hour clock. the 12-hour clock usses a.m and p.m to distinguish between morning and afternoon. with the 24-hour clock,times from 00 00 to 12 00 refer to the morning and times from 12 00 up to 24 00 refer to afternoon or evening
The system used in the modern world is as follows :
60 seconds is one minute,
60 minutes is one hour,
24 hours in one day.
There are two common ways of describing the time of day: the 12-hour clock and 24-hour clock. the 12-hour clock usses a.m and p.m to distinguish between morning and afternoon. with the 24-hour clock,times from 00 00 to 12 00 refer to the morning and times from 12 00 up to 24 00 refer to afternoon or evening
DIGITAL CLOCK :
A digital clock is a type of clock that displays the time digitally (i.e. in numerals or other symbols), as opposed to an analog clock, where the time is indicated by the positions of rotating hands. Digital clocks are often associated with electronic drives, but the "digital" description refers only to the display, not to the drive mechanism.
A digital clock is a type of clock that displays the time digitally (i.e. in numerals or other symbols), as opposed to an analog clock, where the time is indicated by the positions of rotating hands. Digital clocks are often associated with electronic drives, but the "digital" description refers only to the display, not to the drive mechanism.
ANALOG CLOCK : Analog clocks indicate time with a traditional clock face, with moving hands. Digital clocks display a numeric representation of time. Two numbering systems are in use; 24-hour time notation and 12-hour notation. Most digital clocks use electronic mechanisms and LCD, LED, or VFD displays.
TRAVEL GRAPHS
Travel graphs are line graphs that are used to describe the motion of objects such as cars, trains, walkers and cyclists.